Cell Biology of the Immune Response

Part 1: Cellular Basis of the Immune Response

00:00:04.01 Hi, my name is Ira Mellman. I'm Vice President of Research on Oncology at Genentech,
00:00:09.09 a large biotechnology company here in San Francisco. Prior to that though,
00:00:13.12 in fact up to 2007 I was a professor at the Yale University School of Medicine,
00:00:17.29 chairman of the Department of Cell Biology and a member of the Ludwig Institute for Cancer Research.
00:00:22.01 During that time and in fact up until today, my laboratory has been
00:00:26.15 very interested in understanding the fundamental mechanisms of membrane traffic.
00:00:30.02 In other words, understanding the movement of cells and membranes
00:00:33.27 and the proteins and lipids that go to comprise those membranes
00:00:37.00 allowing them to work together to make cell shapes and cell functions of various sorts.
00:00:43.00 The last, more recent period of time though, we've become increasingly interested
00:00:47.27 in trying to understand how membrane traffic acts in highly specialized cells to allow them
00:00:53.16 to carry out the variety of important and specialized functions that are associated with specific
00:00:59.05 and more complex systems. The system that we have chosen to work with
00:01:03.02 over the last several years is the immune system, trying to understand how membrane traffic conspires
00:01:09.06 to get cells of the immune system to work and work together to generate an immune response.
00:01:14.02 It's a terrific problem of cell biology which almost inexplicably to me, at least,
00:01:18.05 has been relatively inaccessible to most cell biologists almost as inaccessible
00:01:22.17 as cell biology has been to immunologists. But nevertheless, there is an enormous amount
00:01:26.29 of very important cell biology to be learned by looking at cells of the immune system,
00:01:30.20 but it also provides a lot more. It provides you with the opportunity to actually understand
00:01:35.27 how events that occur at the molecular level and at the cellular level
00:01:39.22 can integrate with each other at the systems level to understand a very complex
00:01:44.09 and important phenomenon, which has a great great deal of relevance with respect to
00:01:49.13 understanding important and very devastating human diseases.
00:01:53.02 Now in order to introduce you to the topic, and let you know what it is you can indeed find out,
00:02:00.00 I have to first review with you some of the basic features of what the immune response is,
00:02:06.05 and how it's organized in its cellular level of organization.
00:02:10.03 So, what is the basic function of the immune system? It seems to be to be able to provide us with
00:02:15.14 protection against a limitless number of pathogens and toxins
00:02:19.07 that one finds in the environment. It's basically conserved in it's most elemental forms across evolution.
00:02:25.16 Invertebrates have a type of immune system and certainly we vertebrates
00:02:29.23 have a type of immune system, which provides us with a terrific amount of protection
00:02:34.16 under normal circumstances to viruses, bacteria, protozoa, and other environmental poisons and allergens.
00:02:42.00 Now, the immune system is extremely good at this and it's also extremely clever.
00:02:46.02 It can kill incoming viruses or incoming bacteria, but it does so in a fashion which avoids the injury
00:02:53.13 to the host, in other words, us, which provides a really important conundrum in
00:02:59.09 understanding how the immune system works. How is it that cells in the immune system
00:03:03.15 can distinguish self from non-self? How can they distinguish
00:03:07.01 the normal cells and tissues of our bodies from the proteins and components
00:03:13.02 that are associated with the protozoa and bacteria and other microbial invaders
00:03:17.07 that are coming in from the outside. This is probably the major fundamental
00:03:21.29 and conceptual problem in understanding the immune system
00:03:24.25 and it's one that undoubtedly will have the cell biological solution associated with it.
00:03:30.02 Now is this complicated? It's absolutely very complicated, but in my view itâ€™s not
00:03:35.03 really any more complicated than anything else,
00:03:37.00 and if you try and understand how the immune system works in cellular terms,
00:03:40.29 through the eyes of the cell biologists, in fact I believe it does become quite accessible.
00:03:45.02 Now, it's worth the effort, as I've said already, because it's not only interesting,
00:03:50.28 but it's of profound importance to understanding and controlling a wealth of
00:03:55.03 important human disorders, infectious disease, is obvious, arthritis,
00:03:59.10 Crohn's disease, asthma, autoimmunity, and quite possibly even cancer.
00:04:04.01 Now the immune system, or immune response rather, consists of two interconnected
00:04:08.08 arms, the innate immune response, or innate immunity, and adaptive immunity.
00:04:14.02 Well innate immunity refers to that portion of the immune response,
00:04:18.15 which is responsible for detecting components shared by all pathogens
00:04:24.27 that we have to deal with as invaders.
00:04:28.00 An interesting concept, in terms of how this might work, and not immediately
00:04:32.15 obvious how it works, but indeed it turns out to be the case.
00:04:35.01 Adaptive immunity is something different. Adaptive immunity
00:04:39.24 refers to the type of immune response that is molecularly crafted to mold and detect
00:04:45.21 individual antigens that are specific to individual pathogens and individual types of pathogens.
00:04:50.21 These two work together in some rather interesting and mysterious ways that we'll
00:04:55.14 go into later, but nevertheless it is important to keep it in mind that there are
00:04:59.10 these two equal and equally important aspects of the immune response:
00:05:03.04 innate and adaptive immunity. Innate immunity was really first discovered
00:05:07.01 by this great scientists of the past, Elle Metchnikoff, shown here working in his
00:05:12.20 laboratory about 100 years ago at the Institut Pasteur in Paris.
00:05:16.00 Metchnikoff's great conceptual advance was the understanding that inflammation,
00:05:22.27 which is what happens after you become infected by the introduction of a bacterium or a virus,
00:05:30.02 this is why your cuts become red and inflamed and hot and painful if they go untreated,
00:05:37.09 this process of inflammation is a protective process of immunity
00:05:41.26 and not a manifestation of the tissues destruction. In other words, as bad as it looks,
00:05:46.01 this is actually a representation of how the body is responding to invading microorganisms,
00:05:52.05 to rid the body of those microorganisms, rather than a reflection
00:05:57.00 of the microorganisms capacity to meet out damage on the hosts tissue.
00:06:03.01 Prior to this point, this idea was completely foreign to scientists.
00:06:10.01 Now the story goes that one of the most important observations that Metchnikoff
00:06:17.09 made was actually made while on vacation on the beach with his family,
00:06:22.03 and like many modern day scientists, who bring their computers with them on vacation,
00:06:27.03 Metchnikoff in the age before computers brought his microscope,
00:06:31.10 and studied the reaction of starfish larvae to the introduction of foreign materials
00:06:38.16 such as bacteria introduced experimentally into the larvae.
00:06:42.02 What Metchnikoff found was that a series of cells would come in
00:06:46.00 and surround the bacterium and in fact, quite visibly, engulf these microorganisms
00:06:52.00 shown here as these red oblong creatures, contained within this cell.
00:06:56.02 He named these cells macrophages, because they were large cells that ate bacteria,
00:07:02.08 macrophage: â€œlarge eater". The bacteria were taken into the interior of the cell,
00:07:08.00 and Metchnikoff further found that if he stained these cells with a dye
00:07:10.02 that partitioned into acidic elements within cells and other things,
00:07:17.00 the bacteria stained red. Further indicating to him, and in fact correctly to us,
00:07:22.26 that the bacteria after they entered into the cell would be delivered to
00:07:26.28 an acidic intracellular compartment, which we now understand and know as lysosomes.
00:07:32.01 Now bear in mind, this was well over 100 years ago,
00:07:35.24 and long before even membranes were truly discovered. Now these bacteria eventually stopped growing,
00:07:42.18 they died after being taken up by the cells, and eventually disappeared
00:07:49.00 and Metchnikoff further understood that as a process of degradation.
00:07:51.02 So what actually happens when a macrophage eats a bacteria or encounters a bacteria is shown here.
00:07:58.01 The response is not only limited to the uptake and intracellular killing of the bacteria, but also
00:08:05.01 these cells secrete a variety of important cytotoxic agents,
00:08:09.03 degradative enzymes as well as protein hormones referred to as cytokines.
00:08:14.01 Cytotoxic agents include important mediators, such as hydrogen peroxide,
00:08:18.28 which is a common disinfectant that is used, but macrophages do this on their own,
00:08:25.05 as well as other types of active forms of oxygen. They secrete an enzyme called
00:08:30.06 lysozyme, which is quite adept at degrading the cell walls of incoming bacteria,
00:08:34.17 and a series of lysosomal enzymes contained within the lysosomal structures of
00:08:39.09 these cells that basically degrade all sorts of other things. As I mentioned,
00:08:43.11 the cytokines that are released by cells, by macrophages after encountering
00:08:48.17 bacteria, some of which you may already know, such as the molecule interferon,
00:08:54.03 macrophages are a prime source of interferon have the effect of recruiting more
00:08:59.03 macrophages and other cells of the immune system to the site of bacterial
00:09:03.01 invasion, increasing the overall level of inflammation, but again,
00:09:06.24 not for the purpose of tissue destruction, but rather to recruit
00:09:10.24 more and more cells of greater complexity and of increased levels of sophistication
00:09:17.00 that help deal with the infection and hopefully eradicate it before it
00:09:20.27 gets out of hand. Now why is it that macrophages and other cells
00:09:26.07 of the innate immune system, such as neutrophils,
00:09:28.17 know to respond to microorganisms? What is it that they are recognizing?
00:09:33.18 So here the story turns to a relatively recent observation
00:09:38.27 having to do with a class of membrane protein receptors found on macrophages
00:09:43.02 as well as other cells, called Toll-like receptors. What are these?
00:09:47.18 The story actually starts a little bit earlier than that, in the work of
00:09:52.07 Catherine Anderson and Carl Hashimoto, who identified the activities associated
00:09:56.25 with a well known gene in Drosophila called Toll. Now Toll was originally identified
00:10:05.26 as acting in early embryonic development in Drosophila, specifying the dorsal
00:10:11.13 from the ventral pole of the early Drosophila embryo. Toll was known to bind to a ligand, called Spaetzle,
00:10:19.07 which activated the Toll-receptor, sending a signal to the embryo
00:10:23.01 allowing this dorsal ventral polarity axis to be established. Here you can see some embryos
00:10:29.16 that either do or do not express wild-type Toll, or members of the pathway.
00:10:35.01 In panel A, all the way on your right, you can see what the normal embryo looks like,
00:10:39.26 and in the absence of functional Toll-receptor or an active Toll-like pathway
00:10:43.03 you can see that these embryos completely disorganized and they don't develop
00:10:49.01 and it is known as a lethal defect early in embryogenesis. Now Toll it turns out also
00:10:57.17 has a role in the adult fly, a quite different role, but one that is no less important
00:11:05.06 in so far as the fly is concerned. Here a different group of investigators,
00:11:10.23 lead by Bruno Lemaitre and Jules A. Hoffmann found that Toll was absolutely
00:11:16.18 required in order to protect adult Drosophila from their pathogens,
00:11:21.20 in this case what you are looking at is a poor dead fly that was unable to combat
00:11:26.00 the fungal infection that you can see here, growing almost as a beard, or a beard of death
00:11:34.01 around this fly's torso because of the absence of a functional Toll-receptor
00:11:41.05 in the fly as the adult. This is really one of the very very first indications
00:11:46.19 that Toll has a role outside of early morphogenesis and also plays an important role in host defense.
00:11:55.01 Now how does it do this? Here is a diagram of what the Toll-receptor looks like in flies,
00:12:01.24 it has a nice extracellular domain with some repeats,
00:12:04.22 it has an intracellular domain that one can presume has signaling molecules
00:12:09.01 or signaling features associated with it, but one of the most interesting features
00:12:14.06 that fell out of the analysis of what this receptor looked like,
00:12:17.18 was that it was very very similar to a receptor for cytokine, called IL-1.
00:12:22.02 Again, another product of the macrophage. And specifically where it was similar
00:12:27.17 was in the cytoplasmic domain, here in the case of Toll, and here in the case of IL-1 receptor.
00:12:34.03 Since it was known that stimulation of IL-1 receptor turned on an inflammatory
00:12:38.21 response from other sorts of studies, it was surmised that
00:12:42.21 indeed the Toll-receptor did much the same thing. So in subsequent years,
00:12:48.11 when Charlie Janeway and his colleagues started looking for the expression of these receptors
00:12:54.21 in vertebrates, they found indeed that there is a whole family of Toll-receptors,
00:12:59.08 and indeed well over a dozen of them are now known that have the same basic organization as
00:13:03.26 Toll does in Drosophila with an extracellular domain that is similar in many ways,
00:13:09.07 but most importantly the cytoplasmic domains that have a large degree of homology
00:13:15.14 to the Toll-receptor in Drosophila as well as to the IL-1 receptor.
00:13:20.01 Now what these receptors do, and the reason they are so many of them
00:13:24.17 is that each one has a specificity for a different microbial component.
00:13:29.01 In each case, the microbe itself needs those components to survive.
00:13:34.00 So here Toll-like receptors are expressed on the plasma membrane,
00:13:40.05 such as Toll-receptor four, or TRL-4 and TRL-5, see various important
00:13:46.00 components associated with bacteria. So TRL-4 sees components associated
00:13:52.15 with the peptidoglycan, a lipopolysaccharide component of bacterial coats.
00:13:58.01 TRL-5 sees a major protein associated with bacterial flagella,
00:14:02.01 both of which are components that are absolutely needed by these bugs in order to survive.
00:14:07.03 They are shared by great many types of bacteria, hence these Toll-receptors
00:14:12.01 recognize these conserved molecular patterns and act as the innate immune system sensor.
00:14:18.03 Another set of Toll-receptors are actually found in intracellular vesicles, endosomes
00:14:23.09 and lysosomes found within macrophages and other cells, examples here are TLR-7 and TLR-8, and -9.
00:14:30.01 And they have a tendency to recognize nucleic acid components
00:14:34.09 such as double-stranded RNA, DNA, and single-stranded RNA,
00:14:38.29 which are associated with other types of incoming pathogens
00:14:41.03 such as both enveloped and non-enveloped viruses. So here you have a complete pattern
00:14:48.20 of conserved receptors that have this remarkable capacity to be able to detect,
00:14:54.19 again, the shared components that can be found with a wide variety
00:14:58.13 of different types of incoming and invading microbes, turning on the macrophages
00:15:03.26 and in fact any other cell that happens to be expressing them.
00:15:06.26 Now the way that this turn-on takes place, or the way that this signaling occurs,
00:15:13.06 perhaps not surprisingly, is similar to the way that stimulation of IL-1 receptor,
00:15:19.26 the cytokine receptor, does it, turning on a series of signaling intermediates leading into the nucleus
00:15:27.03 activating I think the most important and simplest element, the so-called Nf-kappa-B pathway,
00:15:33.01 which leads to in turn a great number of events that prime
00:15:38.27 almost everything important that happens in the context of an innate immune response.
00:15:44.02 So intracellular signaling pathways are all activated by TLR receptors,
00:15:49.21 the pathways themselves can be different from TLR to TLR as they can from cytokine to cytokine,
00:15:56.13 but this really summarizes the basic feature of how the system works.
00:15:59.02 Now the consequences of it are shown here, here what you are looking at is a video
00:16:04.24 of macrophages that have been given yeast to play with, and what you can see
00:16:11.11 is that the macrophages move towards the yeast and then engulf them.
00:16:16.00 So here is one that is moving directly towards it, and engulfs it. Here is another yeast
00:16:20.19 that is here, which will eventually be attacked and eaten by another macrophage,
00:16:24.10 shown right there, so in much the same way that Metchnikoff found
00:16:28.03 these invading microorganisms activated the macrophage, turned it on,
00:16:35.28 increased its capacity for migration, its capacity for cytotoxic killing,
00:16:41.14 and as shown here its capacity for actually killing and eating the invading microorganisms.
00:16:49.00 This is another movie showing that the process of phagocytosis of these yeast,
00:16:57.17 or in fact any other large particle that a macrophage encounters,
00:17:00.15 is intimately associated with the ability of the macrophage to polymerize actin
00:17:08.03 as a motile cytoskeletal component directly underneath where the particle binds
00:17:14.02 and turns on itself, growing out long pseudopods that engulf the particle,
00:17:20.12 capturing it and bringing it inside the cell, and eventually getting it to fuse with lysosomes,
00:17:25.09 again shown here. So what you are looking at in this particular video is a particle
00:17:31.02 that is entering a macrophage whose surface is stained green and shortly after internalization,
00:17:38.12 this green membrane turns red as a consequence of fusing with these
00:17:43.06 red endocytic vesicles that are found inside the macrophage.
00:17:47.02 Again, showing that very high tech components which Metchnikoff knew over 100 years
00:17:53.22 ago, which is that macrophages can detect, can bind, internalize,
00:17:58.24 and to deliver to lysosomes for purposes of degradation those incoming bacteria and
00:18:05.03 other sorts of pathogens that are found in the outside world against which we need protection.
00:18:09.02 So to summarize then, Metchnikoff really has to be credited with providing us
00:18:16.02 a great deal of not only conceptual understanding, but in many ways even
00:18:19.25 experimental detail that has defined for us the innate arm of the immune system.
00:18:25.03 The system that recognizes shared pathogen-derived components that are recognized
00:18:30.04 by Toll-like receptors as well as a variety of related receptors that
00:18:33.27 we won't have a chance to talk about. And it is powered to a very large extent by cells
00:18:40.16 which are referred to collectively as phagocytes and these include
00:18:44.19 the macrophage, which are the large cells that Metchnikoff first identified
00:18:48.02 as well as neutrophils, or granulocytes, polymorphonucleocytes,
00:18:53.15 which are actually smaller than macrophages, and indeed Metchnikoff had seen these too,
00:18:58.12 he referred to them as microphages. These mediated protection by
00:19:02.05 activating cytotoxic mechanisms, and as you have seen, quite graphically,
00:19:05.19 by actually physically eating, clearing, and degrading extracellular bacteria
00:19:10.24 and other types of microorganisms. Now, almost at exactly the same time
00:19:15.05 that Metchnikoff was working, elsewhere in Europe another
00:19:19.07 terrific scientist, Paul Ehrlich, was also hard at work
00:19:24.01 and you can tell from this image that Ehrlich was a terrific and great scientist
00:19:29.06 because he has one of the hallmarks of great scientists, which is an incredibly messy office.
00:19:34.00 So here he is sitting, reviewing some notes, and what Ehrlich's contribution was,
00:19:41.20 was to show for us how the other main arm of the immune system was organized and what it did.
00:19:49.03 This is called "adaptive immunity". What Ehrlich identified was that individuals,
00:19:56.10 whether it be the humans, it be the animals, that are immunized with various types of microorganisms
00:20:02.03 or bacterial derived toxins, make a response in the blood that is inherently protective,
00:20:10.06 and in fact Ehrlich coined the term "antibodies" to describe this response,
00:20:15.01 which has the ability, obviously, of protecting us against whatever it is that had entered
00:20:20.27 into our systems or into our bloodstreams.Antibodies see individual antigens
00:20:26.27 that are specific to individual pathogens types, so if you immunize with one type of bacteria,
00:20:33.02 you will not necessarily make antibodies that will recognize and protect a second individual
00:20:38.02 against another type of bacteria. So in this way, the system is fundamentally different
00:20:43.21 from the innate immune system. It's crafted in a molecular fashion
00:20:47.22 to the molecular entity that happens to be coming in. The way the cellular
00:20:54.00 mechanism, whereby the adaptive immune system works, is using not so much
00:20:58.11 macrophages, as we know now, but rather making use of antigen-specific
00:21:02.21 lymphocytes that indeed make these antibodies that recognize and kill the infected target cells
00:21:08.03 either separately from, or as you will see in a minute, in conjunction with the macrophages.
00:21:14.01 This is what an antibody molecule looks like in crystal structure. It consists of two major parts
00:21:21.04 a Fab fragment and a Fc fragment, both of which are linked together,
00:21:26.01 the molecular weight is about 150,000 Daltons and consists of four chains:
00:21:31.28 two light chains, shown in red, and two heavy chains shown in yellow and in blue.
00:21:37.01 The antigens themselves actually bind to the so called Fab regions of antibody
00:21:45.26 molecules, demonstrated in this diagram, out near the tips. So here you find a
00:21:50.26 great deal of sequence variation that allows the antibody to form complementary structures
00:21:56.02 allowing it to interact quite specifically with whatever antigen comes into an organism,
00:22:04.03 against which an antibody can be made. Now how antibodies work.
00:22:10.01 After recognizing their antigen, they are made, and as shown here they'll bind
00:22:16.03 to the antigen and this particular example that antigen is present on the surface of the bacterium,
00:22:21.20 and one of the simplest ways in which the antibody can work to kill
00:22:25.29 the bacterium is to recruit another set of proteins that are found in our plasma
00:22:31.00 called complement, which actually is a number of proteins, not just one. Complement is
00:22:37.00 recruited by antibodies, inserted into the bacterial membrane causing
00:22:41.23 the bacterium to lyse. Now in addition, these antibodies will work together
00:22:46.02 with element of the innate immune system, macrophages in particular,
00:22:49.26 but also neutrophils. Macrophages are probably more important
00:22:53.00 since macrophages actually have receptors for the Fc domains of these antibodies,
00:22:58.04 which have some of the same effects that Toll-receptors do,
00:23:02.01 in other words binding of antibody coated microorganisms to macrophages will trigger
00:23:06.24 the release of the same types of cytotoxic compounds that we've already discussed
00:23:11.01 and also trigger the ability of the macrophage to mediate phagocytosis
00:23:15.17 and intracellular killing and destruction of these antibody associated
00:23:21.09 or antibody coated microorganisms. So here you have this nice example of the innate system
00:23:26.12 working together with the adaptive immune system. Now antibodies are not made by
00:23:31.20 macrophages, although that was an idea that was originally thought of by
00:23:36.01 Metchnikoff and by Ehrlich who by the way shared the Nobel Prize
00:23:39.11 for their discoveries back in 1908, 100 years ago this year. Antibodies instead
00:23:45.16 are made by lymphocytes, a particular class of lymphocytes, as many of you know I'm sure,
00:23:49.27 called B lymphocytes. B lymphocytes exist in great number found throughout
00:23:57.22 a variety of lymphoid tissues in the body, and have a repertoire
00:24:04.03 of potential interactions, in other words, due to inherent and preexisting variability in
00:24:10.11 that small Fab region, or complementarity determining region
00:24:15.01 found in the Fab region of antibody molecules, incoming antigens can find or B cells
00:24:23.13 rather with the right specificity can find and actually bind to
00:24:27.00 antigens associated with bacteria, or antigens that are simply with soluble proteins,
00:24:32.09 and the simple act of binding of the antigen to the antibody,
00:24:37.03 which at this point in a B-cell's development is actually a membrane protein receptor
00:24:41.02 on the B-cell, is sufficient to simulate development of the B-cell and finally the
00:24:46.22 production of an amplification of more and more of these antibody molecules.
00:24:51.03 Now this is a video that shows you how the system works, when you get a sore throat,
00:24:57.27 which is indicated here in red. What that's again a manifestation of,
00:25:02.27 as Metchnikoff told us, a protective response, not a destructive response.
00:25:07.01 So here you see bacteria lining the surface of your throat following an infection
00:25:14.02 and these bacteria are putting off a variety of protein antigens that are associated with these bacteria,
00:25:22.03 so not only have you generated an innate immune response,
00:25:25.24 but now these bacterial specific antigens are being released and what happens to them is that they begin
00:25:33.13 to drain into the intercellular spaces, that one finds in all of your tissues
00:25:39.08 referred to as the lymph. The lymph drains into the lymphatics,
00:25:42.25 which then comes into these nodes, or specifically lymph nodes that monitor every 24 hours a day
00:25:52.04 what proteins, what antigens, what bacteria have entered into the lymph.
00:25:57.03 So here you see our bacterial protein entering into the lymph node, and what they
00:26:02.07 encounter here are the wide array of lymphocytes and other cells and here you can
00:26:08.01 see them in a higher magnification and as our bacterial derived proteins come in,
00:26:12.26 they filter through these millions or billions of cells as you can imagine,
00:26:20.22 and cells that are B-cells that may detect a component of that antigen will bind to it,
00:26:29.23 based on these antibody molecules or via these antibody molecules
00:26:33.07 that are intercalated as membrane proteins on the surface of these early B-cells shown here
00:26:38.19 clicking on, and this will then hit onto another B-cell receptor, and a third
00:26:45.05 and a fourth, until enough of them come together to actually generate a signal
00:26:50.00 to the B-cell, which says that I have now detected the antigen I was born to detect
00:26:57.10 and as a result, it is now time to start making more of myself. So these B-cells
00:27:03.23 become very active and begin to develop and divide.
00:27:10.29 The affinity that they have for the individual antigens, in essence, increases as B-cells with increasingly
00:27:20.24 large affinities, increasingly great affinities for antigens,
00:27:24.07 compete with each other to bind more and more. So here you see a clone of B-cells that gives rise
00:27:31.07 to a larger number of itself and then as you can see here, in this representation,
00:27:39.13 antibody molecules begin to be released into the extracellular space
00:27:44.19 and here is just an indication of the secretory event that takes place very similar
00:27:51.10 to that which is described in another of the iBioseminar science series given by Randy Schekman.
00:27:59.01 Now here the antibody molecules at this stage in development are actually pentamers
00:28:04.00 coming back homing to the bacteria, coating them with antibody molecules,
00:28:09.11 recruiting complement, and, as shown here also recruiting macrophages,
00:28:13.28 which again, just as Metchnikoff has already shown us, will come and eat those
00:28:18.08 bacteria that are coated with antibody taking them up by phagocytosis,
00:28:21.27 killing them and degrading them. Now it turns out that things are not that simple,
00:28:29.28 of course. What I've just shown you in that video isn't in every sense correct,
00:28:37.20 but it turns out that B lymphocytes make the best antibodies when they are helped
00:28:41.02 by another type of lymphocyte, referred to T, or thymus-derived, lymphocytes.
00:28:46.18 And the way that works is that here you can see an extracellular antigen coming,
00:28:50.28 binding to the surface antibody molecule of B-cells and then it turns out that
00:28:56.09 the antigen is internalized by endocytosis into the B-cell, and a small fragment
00:29:01.23 of this antigen is cleaved off and is bound to a molecule referred to as a major
00:29:07.02 histocompatability class II molecule, or MHC class II molecule. This complex of the
00:29:13.17 peptide plus the MHC class II molecule is then recognized by a preexisting T-cell,
00:29:19.26 which has a different type of antigen receptor referred to as the T-cell receptor,
00:29:24.11 again which has a great deal of diversity built into it as a consequence
00:29:30.24 of the development of T-cells in the early development of the immune system
00:29:37.09 and what the T-cell then does, is to secrete again our friends the cytokines,
00:29:41.06 in this case a class of cytokines, which helps the B-cell develop, helps them
00:29:47.28 divide even more, and helps them create antibodies with every increasing affinity.
00:29:54.22 Now the way the T-cell system works, is illustrated in a little bit more detail here.
00:30:00.08 T-cells come in two general flavors, and we'll come back to this later,
00:30:04.28 CD4 T-cells, as well as CD-8 T-cells. We've been talking about CD-4 T-cells,
00:30:09.27 which recognize bacterial or other derived peptides bound to these so-called MHC class II molecules,
00:30:16.23 and they do this by the virtue of having these T-cell receptors, which again have
00:30:22.14 their own specificities associated with them, such that by random chance,
00:30:28.08 the appropriate T-cell receptor is made for this particular complex of peptide and MHC class II.
00:30:36.00 Diversity in the T-cell receptors, rather than being so much generated by mutation,
00:30:41.00 which is what occurs in the antibody in the B-cell system, occurs by
00:30:45.11 rearrangement of the T-cell receptor gene, again rearrangements that cause a greater number of
00:30:53.15 potential combinatorial sequences that can recognize a wide array
00:30:57.27 of these peptide MHC complexes. So that said CD4 T-cell sees MHC class II molecules to a large
00:31:06.04 extent because it makes the second membrane protein called CD4,
00:31:09.17 which also recognizes the MHC class II molecules, but recognizes an invariable portion
00:31:16.01 of those molecules. CD8 T-cells express exactly the same type of T-cell receptors,
00:31:22.02 but they're targeted to a different type of MHC molecule, in this case a MHC class I molecule
00:31:28.01 and the reason this particular targeting takes place is because the CD8 membrane
00:31:33.01 protein found on the CD8 T-cell, recognizes the class I molecule and not the class II molecule.
00:31:41.01 So very complicated and this is obviously a simplistic view of how this works,
00:31:47.10 but at its most elemental form, this is how T-cells cooperate with B-cells
00:31:52.27 and in fact with a variety of other cells as well. Now CD8 restricted T-cells
00:32:00.28 or those T-cells that see antigens bound to class I in general don't see antigens
00:32:07.07 that are coming in from the outside. In much the same way,
00:32:11.11 or at least I should say, analogous to what happens in the case of Toll-like receptors
00:32:16.06 that are expressed either on the surface of a cell or inside, the CD4/CD8 system, or class I and class II
00:32:23.08 MHC systems are adapted to incoming pathogens that reveal themselves
00:32:28.04 either on the outside world or on the inside world. The CD8 system and the class I system
00:32:33.28 take care of those things that are going on in the inside world.
00:32:37.01 So when viruses infect our cells, those viruses almost invariably work by binding to
00:32:43.14 receptors on the surface of the cell and fusing, or entering, the cell
00:32:48.25 either at the level of the plasma membrane or following entry into endocytic vesicles,
00:32:53.22 and then breaking out into the cytoplasm. That type of endogenous pathogen,
00:33:00.16 because you can now refer to it as endogenous because it's found inside the cell,
00:33:06.15 that type of pathogen is treated by the immune system to generate peptides
00:33:11.29 that are then loaded onto class I as opposed to class II molecules. Now the way
00:33:17.13 these T-cells work, again, is somewhat analogous to what one finds in the
00:33:22.09 innate immune system, except that it is all very specific and very antigen driven.
00:33:26.01 So here you are looking at a cytotoxic CD8 positive (+) T-cell,
00:33:30.15 this is work of Julian Griffin at the University of Cambridge in England, and what Julian
00:33:36.18 has noticed as well as others over the years is that these cytotoxic CD8+ T-cells, when they recognize
00:33:44.07 a virus-infected target in fact polarize all of their lysosomes,
00:33:50.08 which actually now are differentiated to contain a wide variety of cytotoxic compounds,
00:33:55.27 towards the infected T-cell. These granules line up at the interface, or synapse,
00:34:02.19 between the T-cell and the target, and are eventually released, killing the target.
00:34:08.01 This is what you are looking at here in an electron micrograph also from Julian's work.
00:34:12.12 Here you can see these cytotoxic T-cell, or CD8 T-cell, or CTL granules
00:34:18.01 in the region of the cytoplasm that is very very close to the infected target cell.
00:34:24.02 These granules contain lysosomal enzymes, various lytic enzymes, ligands
00:34:30.04 such as Fas and receptors that will induce apoptosis or cell death in the target,
00:34:36.01 and also perforating molecules called perforins among others that will punch holes
00:34:43.10 in the target cell. All leading to its rapid death. So in other words, the virus has
00:34:48.15 infected this cell, think its safe by existing within the cell and then the cytotoxic
00:34:52.16 T-cell comes along and recognizes a peptide derived from the virus,
00:34:56.17 releasing the granules at the site of the infected cell, thereby killing the cell.
00:35:02.02 This is just the diagram showing how this process works. In fact over the last several
00:35:07.16 years, as a consequence of interrogating some important mutations
00:35:11.13 that lead to defective CD8 T-cell responses, which Julian and others have shown,
00:35:17.00 is that these granules actually have to physically polarize by moving on microtubule tracks
00:35:22.19 from diverse places within the cytoplasm to this interface, this synapse,
00:35:27.14 between the T-cell and its target. In the absence of genes that are required
00:35:33.10 for the translocation of these granules to this point in the cell, Rab proteins,
00:35:40.02 microtubule binding proteins, etc. these T-cells are incapable of docking
00:35:47.11 with or incapable of fusing with the plasma membrane of the T-cell close to the target.
00:35:54.02 Again, emphasizing one critical element of where membrane traffic
00:35:58.25 plays a major role in allowing the immune system to conduct its job.
00:36:03.00 Now how does this all work, we've discussed already a bit how TLR's activate
00:36:11.16 cells such as macrophages in the innate immune system. T-cells become activated
00:36:16.20 in two very important ways. The T-cell receptor itself is a signaling molecule,
00:36:23.01 recruiting tyrosine kinases to its cytoplasmic domain after it recognizes its ligand,
00:36:29.22 which as we've been discussing is a complex of peptides plus MHC molecules.
00:36:34.00 But also a variety of other interactions take place so-called co-stimulatory receptors
00:36:41.02 which are other receptors that are present on the surface of T-cells,
00:36:45.02 recognize a variety of other molecules that can be found on the surface of infected cells
00:36:49.28 or on B-cells or on other cells of the immune system, that send further signals
00:36:54.24 to the T-cell, enabling it to more effectively do its job and also amplify its own
00:37:01.03 numbers in a way that is selective and antigen driven,
00:37:05.12 quite analogous to what happens in the case of B-cells. Further, selected cells in the immune system
00:37:12.05 which are referred to as antigen-presenting cells or APCs,
00:37:15.22 which we'll come back to in a later lecture are capable of secreting their own sets of cytokines,
00:37:22.13 which have the effect of further accentuating and enhancing T-cell responses.
00:37:27.01 So here we have two aspects, two critical aspects of the immune system.
00:37:32.04 Innate immunity, which is characterized by direct cellular responses
00:37:37.09 to pathogens by detecting shared microbial patterns that is not antigen specific,
00:37:43.09 working together hand in glove with Ehrlich's observation of the adaptive immune response,
00:37:50.20 which generates specific antibodies to variable antigens,
00:37:54.01 and occurs as a consequence of an antigen stimulation of T-cells and B-cells. These two things,
00:38:01.09 as I've already intimated to you are connected, but they're connected in even a more intimate
00:38:06.01 fashion, which we'll turn to in the next lecture, provided by a recently identified
00:38:11.10 cell type referred to as the dendritic cell, which really we now understands
00:38:15.16 provides the long sought after missing link between the innate and adaptive immune system.

Part 2: Antigen Presentation and Dendritic Cells

00:00:01.00 Hi, Ira Mellman again from Genentech. I'd like to continue our discussion
00:00:05.24 of the cell biology of the immune response, this time turning to specifically
00:00:09.22 the problem of antigen presentation and the role of dendritic cells
00:00:13.17 in linking the two aspects of the immune response
00:00:16.06 that we've already discussed, innate immunity and adaptive immunity.
00:00:19.00 Innate immunity having been discovered by Metchnikoff
00:00:21.29 and adaptive immunity by Ehrlich all about 100 years ago.
00:00:25.00 Now in order for T-cells to do their job helping B-cells respond by
00:00:31.15 making antibodies and also by helping to kill virus infected cells and other types of pathogens,
00:00:37.13 they themselves require a significant amount of help, which is provided
00:00:43.03 by the so-called antigen presenting cells or APCs. Now recognition of T-cell
00:00:49.17 receptors of their targets does not necessarily lead to cell killing.
00:00:55.00 In fact this is an interaction that has to take place in order to generate a sufficient number
00:01:00.01 of T-cells to mediate the immune response in the first place. So the signal
00:01:04.01 that is sent by the T-cell receptor to the T-cell is a consequence
00:01:08.22 of seeing its ligand serves to activate the cell to not only to kill but also to differentiate
00:01:16.21 and divide, again depending on the type of T-cell you happen to be.
00:01:20.00 These types of signals together with other types of signals provided by other types of
00:01:25.07 membrane proteins referred to as co-stimulatory molecules,
00:01:28.21 are provided by a class of cells referred to as APCs or antigen-presenting cells.
00:01:35.00 Now as we reviewed in the last lecture, T-cell receptors see two different types
00:01:40.29 of peptides, peptides bound either to MHC class II molecules or peptides bound
00:01:46.09 to MHC class I molecules. CD8 T-cells recognizing the class I molecules,
00:01:51.16 CD4 T-cells recognizing the class II molecules. This is a structural
00:01:56.20 representation of how the recognition of the peptide MHC complexes by T-cell receptors actually occurs.
00:02:04.00 So here in the upper level you see the T-cell receptor itself,
00:02:07.07 the two major antigen recognition elements of it, the alpha chain and the beta chain,
00:02:12.00 which form a complex that is specifically adapted to recognize that a particular peptide
00:02:17.03 bound to a particular MHC molecule so here you can see the peptide,
00:02:21.04 which usually ranges in 9 to 10 or more of amino acids in length,
00:02:26.21 nestled within a very specific peptide binding cleft found in this case in a MHC class I molecule
00:02:34.00 that is expressed by the antigen presenting cell expressing in turn the antigen from
00:02:39.18 which this particular peptide is derived. In order for this system to work,
00:02:43.23 it has to be amplified, it has to be selected, the T-cells have to be amplified
00:02:48.11 and have to be selected and have to be affinity matured in such a way
00:02:51.28 that they can detect their peptides with higher and higher affinity
00:02:55.14 continuously again sculpting these T-cell receptors. Now producing
00:03:00.23 the peptide MHC complex, which is obviously key to this entire process
00:03:04.00 is a job of the antigen presenting cell. Now how does the antigen presenting cell do this?
00:03:10.27 We've already talked about the fact that there is both a class I and a class II
00:03:15.28 dependent pathway or restricted pathway of antigen presentation.
00:03:21.00 The class II pathway is predominantly adapted to presenting those molecules
00:03:26.27 derived from extracellular pathogens such as extracellular bacteria or proteins,
00:03:33.11 toxins, whatever are released from bacteria. So in those cases what happens
00:03:38.16 as we already discussed in the case of B-cells, the antigens bind to the surface
00:03:42.26 of the cell, the antigen presenting cells are taken up and deposited
00:03:47.16 within endocytic vesicles within the cytoplasm of the APC.
00:03:53.11 Here the antigens are unfolded, unwound, and eventually degraded into peptides
00:03:59.04 that are loaded also in endocytic vesicles onto the class II molecules themselves.
00:04:03.00 Now how the class II molecules get there is a rather remarkable story
00:04:08.01 and a remarkable piece of cell biology and membrane traffic in its own right.
00:04:11.00 Class II molecules are membrane proteins and like almost all other membrane proteins
00:04:15.27 begin their lives at the level of the rough endoplasmic reticulum,
00:04:19.05 where they are synthesized and inserted across the ER membrane
00:04:23.00 and assembled together with a chaperone called the invariant chain in the ER
00:04:28.04 that then after assembly takes place gets transported from
00:04:32.06 the endoplasmic reticulum into the cis-golgi, through the golgi stack, emerging at the
00:04:37.13 trans-side of the golgi complex but unlike proteins that are destined for
00:04:44.10 secretion or destined to be inserted into the plasma membrane,
00:04:48.02 MHC molecules are diverted from this constitutive secretory pathway and instead
00:04:52.28 are taken into the endocytic compartment where the invariant chain is removed
00:04:57.15 and we'll come back to that in a moment, and the class II molecule rendered accessible
00:05:01.11 to the peptides that can be derived from the incoming antigen.
00:05:05.17 Following binding of the peptide to the class II molecule, this complex is taken to the cell surface
00:05:11.15 where it can now be recognized by CD4+ T-cells.
00:05:16.00 Now the class I pathway as we've discussed services predominately those antigens
00:05:21.24 that are self-synthesized by a given cell. This of course can include
00:05:28.01 any membrane protein or cytosolic protein that is synthesized as a
00:05:33.01 consequence of the viral infection. So in the case of cytosolic proteins, these proteins are made,
00:05:39.06 ubiquitinated, degraded in the cytosol by the proteosome and peptides
00:05:43.25 that are produced by the proteosome were transported into the ER, where they are then bound
00:05:48.07 to class I molecules that are again, transported from the ER to the golgi
00:05:52.05 but now rather than going to the endocytic compartment,
00:05:55.00 instead the class I molecules go directly to the cell surface. Now all antigen presenting cells
00:06:00.20 are not created equal. There are amateurs and there are professionals.
00:06:04.00 Amateurs can make the class I response in most cases, because MHC class I molecules
00:06:10.23 are expressed by virtually all nucleated cells in the body so therefore virtually
00:06:15.09 all nucleated cells are protected by the immune system against infection
00:06:19.22 by viruses, which is a good thing. The MHC class II system on the other hand
00:06:24.20 is synthesized and expressed only by a relatively restricted number of cells
00:06:29.14 in the body. In most cases our cells that are specialized cells in the immune system
00:06:35.05 B-cells, macrophages, and most importantly these dendritic cells
00:06:39.23 that we mentioned earlier. Now dendritic cells are really special
00:06:43.24 and in fact are the professionals professional. They are the Tiger Woods
00:06:48.05 of the antigen presenting cell universe. Why? Because they are by far the most efficient.
00:06:54.14 They can capture almost meaningless and non-existent amounts of antigens
00:06:58.22 and turn those antigens into small peptides that can stimulate T-cell responses. They have
00:07:05.28 the rather unique capacity to be able to capture antigen from
00:07:10.17 wherever in the body antigen is first introduced,
00:07:14.12 be it in the skin, in the lung, in the intestine wherever the antigen is captured
00:07:19.07 and then its not simply left to passive transport through the lymphatics to go back to the lymph nodes,
00:07:25.05 but rather these cells are adapted to hone in on the lymphatics and make a bee line directly
00:07:30.10 into the lymph nodes where the dendritic cells can find a huge accumulation
00:07:35.29 of both T-lymphocytes and B-lymphocytes and help their stimulatory events take place.
00:07:42.12 Perhaps most importantly, dendritic cells are the only cells in the immune system,
00:07:47.13 the only antigen presenting cell that can actually initiate the antigen specific
00:07:51.10 immune response. In other words, prior to the advent of the first of an antigens kind
00:08:00.15 coming in before you had your very first infection with influenza
00:08:05.12 you may have T-cells that are capable of responding to influenza virus,
00:08:09.00 but they are naÃ¯ve, they don't really know what to do. Only the dendritic cell can wake
00:08:14.16 them up. If you delete dendritic cells from a mouse using a variety
00:08:20.07 of genetic knockouts, you find those mice are almost completely incapable
00:08:24.12 of mounting antigen specific immune responses. Why? Because only
00:08:29.08 the dendritic cell can present an antigen at a sufficient level of efficiency and with
00:08:36.27 a sufficient amount of stimulation provided to the T-cell in order to wake the T-cell up
00:08:41.29 and get the T-cell response going. Now the other side of the coin here though
00:08:48.02 is the issue of tolerance in the sense that remember one of the key abilities
00:08:54.03 of the immune system is to be able to mount virulent cytotoxic responses
00:09:00.03 protective responses to invading pathogens, but somehow minimize
00:09:05.01 if not avoid entirely destructive components that are directly against our self antigens
00:09:12.00 in other words our own tissues and selves. Dendritic cells play also a key role
00:09:17.09 in ensuring that our immune system maintains tolerance to self antigens
00:09:22.21 and we'll come back at the very end to discuss some of the more recent ideas
00:09:27.21 on how we think that takes place. Now probably though the most important
00:09:33.02 key conceptual element of how the dendritic cell system works
00:09:37.16 and why dendritic cells play such a role that is so important in linking the innate and
00:09:42.27 adaptive response is that like cells of the innate response, innate immune response,
00:09:48.13 dendritic cells can respond to exactly the same types of microbial signals
00:09:52.12 as do the macrophages. Again, by virtue of the fact that they express
00:09:57.07 the same classes of Toll-like receptors that macrophages do, but instead of under
00:10:02.28 most circumstances emitting cytotoxic compounds as a consequence of that,
00:10:07.01 they turn the information and the advent of microbial pathogens
00:10:14.05 coming into the system into the peptide language that can be understood by T-cells,
00:10:19.08 thereby linking the activation of the adaptive response
00:10:25.09 to the activation of the innate response. So then as I'm mentioning in words,
00:10:30.18 as you can see here, dendritic cells do play this really important missing link
00:10:35.21 that intimately connects innate immunity with adaptive immunity responding
00:10:41.04 to the innate signals and turning those signals into the language of the adaptive immune response.
00:10:47.00 Now this is a concept that is relatively new and certainly not nearly as
00:10:54.13 old meaning 100 years, as the first discovery of the adaptive response
00:11:00.14 and the innate response. It took almost 80 to 100 years later to really figure this out,
00:11:05.26 and that was done by this gentleman with no beard, Ralph Steinman,
00:11:10.20 who works at the Rockefeller University who was really among the very very first
00:11:14.23 to appreciate that dendritic cells have this remarkable role in being able to have a critical element
00:11:23.15 in linking the innate and adaptive responses by being just so powerful and so special
00:11:29.23 and so adept at generating T-cell responses in response to antigens
00:11:37.05 and in response to adjuvants or microbial products. Now the basic logic of
00:11:42.11 the dendritic cell system is shown here, and this is terrifically rich and complex
00:11:46.23 but indeed quite understandable. The idea is as follows, dendritic cells exist
00:11:52.22 as immature sentinels in a variety of peripheral tissues, in fact all of our peripheral tissues
00:11:58.05 contain dendritic cells. Here we are looking at the skin, at the epidermis,
00:12:02.02 where dendritic cells are intercalated in various levels in the skin,
00:12:06.27 most interestingly in the epidermis itself where these long stellate cells
00:12:12.00 are intercalated among the far more numerous keratinocytes. Indeed, the fact that these dendritic cells
00:12:19.18 existed in the skin is actually a fairly old observation made by Paul Langerhans
00:12:25.15 also who was responsible for having first identified the islets of Langerhans in the pancreas,
00:12:31.07 but Langerhans didn't know what these cells did, but indeed he identified that they were there.
00:12:36.01 We now know that they are present in the skin for the purposes of immune surveillance.
00:12:42.02 They are there to capture incoming antigens, to capture incoming pathogens,
00:12:47.18 and after that capture takes place they migrate out from the skin, enter the lymphatics,
00:12:52.28 and eventually as I already mentioned find their way into lymphoid organs
00:12:58.26 where they also now start to intercalate together with lymphocytes T-cells and B-cells.
00:13:06.00 Now by the time they get to lymphoid organs under most circumstances,
00:13:10.24 these dendritic cells change in their characteristics, they become mature.
00:13:16.21 The difference between an immature cell and a mature cell turns out to be key
00:13:21.25 in understanding exactly what happens and we'll come to that in just a moment.
00:13:26.00 Immature dendritic cells and mature dendritic cells differ from one another
00:13:31.17 in some very very important ways. Immature dendritic cells are shown here
00:13:36.05 in an immunofluorescence picture. What you can see is that all the MHC molecules,
00:13:40.24 particularly the MHC class II molecules that are expressed by
00:13:43.28 immature dendritic cells are sequestered inside the cell in lysosomes and late endosomes.
00:13:50.00 They are not at the surface, so as a result these immature DCs are relatively speaking
00:13:57.08 incapable of stimulating T-cells. In addition they don't express co-stimulatory
00:14:02.27 molecules, they're very poor at secreting cytokines and they are
00:14:07.03 relatively non-motile, so as a result they are very poor at T-cell stimulation.
00:14:12.20 What they are good at though is antigen accumulation. So we view these
00:14:16.15 cells as the sentinels that are the first ones that encounter antigen in the periphery
00:14:20.18 and then as a consequence of detecting antigen and also having the ability
00:14:27.09 to detect the innate signals encompassed or encoded in those antigens
00:14:32.06 via Toll-like receptors and other inflammatory product receptors these
00:14:37.20 dendritic cells change their morphology and also change their function
00:14:41.10 dramatically and really can do so in a remarkably short period of time.
00:14:45.16 We find that only a relatively few hours is required to transform a cell
00:14:51.14 that looks like this to a cell that looks like this, one that extends out enormous
00:14:57.00 dendrites that give them their name, that now relocate all of the
00:15:01.12 class MHC molecules that were present in lysosomes to the surface of the cells
00:15:06.11 and also induce the expression of a variety of other important molecules
00:15:11.14 such as these co-stimulatory molecules that are necessary for optimal T-cell stimulation.
00:15:18.26 So the mature dendritic cell is the cell that is most adept at antigen presentation
00:15:24.00 and antigen stimulation. This flip from the immature to the mature state
00:15:28.27 is intimately linked to the fact that the immature dendritic cell expresses
00:15:34.14 these Toll-like receptors. Were it not for that fact, not for the fact that
00:15:39.07 these cells that are intimately associated with the adaptive response
00:15:42.22 also have the capacity to respond to the most fundamental and
00:15:47.24 elemental element of the innate response we would not have this link. So it's actually
00:15:54.14 maturation that does this. Now as cell biologists interested in membrane traffic
00:15:58.19 we've been very interested over the years as have been many other groups
00:16:02.16 in trying to understand what's responsible for this dramatic morphogenetic
00:16:07.00 change that dendritic cells exhibit and how does it relate to the function
00:16:11.18 of these cells and how to these functions relate to the overall control
00:16:15.18 of the immune response. So here on the left you are looking at a diagram
00:16:20.09 of the membrane traffic phenotype if you will of an immature dendritic cell.
00:16:25.07 These are cells that are highly endocytic, they take up lots of antigen
00:16:29.20 by a variety of different mechanisms of endocytosis, those antigens come in from
00:16:33.25 the outside, find their way to endosomes and finally to lysosomes
00:16:37.13 where quite remarkably they sit unlike most other cells that degrade
00:16:41.20 very rapidly proteins and nucleic acids and lipids and carbohydrates
00:16:46.04 that make it into lysosomes in immature dendritic cells the antigen that enters lysosomes
00:16:52.24 is protected and protected from degradation. At the same time,
00:16:57.24 these cells are making a large number of MHC molecules, particularly MHC class II molecules
00:17:03.17 which instead of being taken to the cell surface where they sit,
00:17:07.26 which is what happens in most other cells, now these molecules as well are targeted to the lysosomes
00:17:12.23 but basically nothing happens, the MHC molecules sit there, the antigen sits there,
00:17:17.10 a little bit of degradation, a little bit of loading of peptide onto the MHC molecules
00:17:22.12 but really not too much takes place until these cells are exposed to a TLR, a Toll-like receptor ligand.
00:17:31.26 In other words, one of the preserved molecular patterns that are conserved
00:17:36.13 from microbe to microbe, then everything starts to change and starts to change really fast.
00:17:42.07 One of the first things that occurs is that endocytosis, at least many forms
00:17:47.27 of endocytosis are shut off to a very large extent, this reflects
00:17:53.09 the fact that these Rho-family of GTPases particularly of the molecules
00:18:00.06 Cdc42 rather than being present in a constitutively active form
00:18:06.06 is now de-activated and present not as the GTP active form but rather as the GDP inactive form.
00:18:14.02 So antigen uptake is not cut-off completely but is diminished.
00:18:17.15 Next thing that happens is that newly synthesized class II molecules,
00:18:21.18 rather than being directed entirely to lysosomes are now taken from the golgi to endosomes
00:18:28.01 and like in other cells for other types of molecules are targeted to the cell surface.
00:18:33.06 There is a lot of reasons for this, we'll come back to one of the most important
00:18:37.01 in a minute but much of it has to do as well with changes in the metabolism
00:18:43.02 of this class II associated chaperone referred to as the invariant chain. As long
00:18:48.06 as the class II molecules associated with the invariant chain the class II molecule
00:18:52.17 is taken to lysosomes. If the invariant chain is removed, the class II molecule can
00:18:57.22 now proceed out to the cell surface. This happens for a variety of reasons,
00:19:02.06 not the least of which is due to down regulation of an antiprotease
00:19:06.13 called cystatin c, which turns off the proteolytic enzyme that is normally responsible
00:19:12.01 for degrading this invariant chain. In fact the lysosomes are activated
00:19:17.27 completely in this case for a variety of reasons, probably one of the most
00:19:23.06 interesting is the activation of lysosomal acidification. Normally
00:19:28.16 lysosomes are acidic vesicles, as Metchnikoff first told us, but in immature dendritic cells
00:19:34.26 they're less acidic than they need to be. The reason for that has been described
00:19:39.22 over the last two or three years as reflecting two key events.
00:19:44.04 One, the vacuolar proton pump or the ATPase that is required to move protons
00:19:50.27 from the cytosol into the lumen of the lysosome thereby dropping its pH,
00:19:56.01 is inactive in the immature dendritic cell. As a consequence of maturation,
00:20:00.24 as a consequence of TLR stimulation, this proton pump
00:20:07.00 is activated by turning on an assembly process, now allowing protons
00:20:12.14 to be translocated from the cytosol into the lysosomal lumen
00:20:16.05 in exchange for ATP hydrolysis thereby acidifying the interior of the lysosome.
00:20:22.10 Sebastian Amigorena in Paris has further found that in some ways like
00:20:26.21 macrophages, dendritic cells are indeed capable of generating active
00:20:30.27 oxygen species but one of the most important features here
00:20:34.23 is not so much to kill the incoming pathogen but rather to further regulate
00:20:39.11 the ability of lysosomes and incoming phagocytic vesicles to acidify their lumens,
00:20:47.02 again emphasizing how important it is to the dendritic cell
00:20:51.21 to ensure that the pH of the compartments involved in antigen presentation
00:20:56.14 and antigen processing are indeed carefully regulated.
00:21:00.08 So this is basically how it works, very simply the lysosomal pH of
00:21:05.19 immature dendritic cells is slightly acidic, it has a pH of 5.5.
00:21:10.07 The lysosomal pH found in organelles of mature dendritic cells
00:21:17.03 is more acidic by one whole pH unit, 4.5.
00:21:20.23 Doesn't sound like a lot but it turns out that most of the lysosomal
00:21:24.15 proteases and nucleic acid degrading enzymes and lipid degrading enzymes
00:21:30.00 that are found in lysosomes have a very sharp pH optimum
00:21:33.18 and they really don't work very well unless the pH that they are working in
00:21:38.08 is below pH 5, so the maturation process then drives the pH down
00:21:43.24 from a pH that's too high for optimal activity of the lysosomal proteases
00:21:48.17 to a pH that now is just right, the goldilocks effect allowing these
00:21:54.03 lysosomal proteases to do their work at optimal levels increasing
00:21:58.15 the efficiency at which peptides can be generated for association
00:22:04.12 with MHC class II molecules. Now this is a diagram just quickly as to how this works.
00:22:10.08 So here you can see a class II molecule that begins its life associated
00:22:15.18 with the invariant chain as you've seen in previous diagrams,
00:22:19.03 it consists of two membrane proteins, an alpha chain and a beta chain,
00:22:23.08 here is the invariant chain in green together with its lysosomal targeting signal.
00:22:28.00 The invariant chain is degraded by a series of proteolytic cleavages
00:22:31.26 most important of which is mediated by an enzyme called cathepsin s,
00:22:36.19 which is found most prevalently in professional antigen presenting cells such as dendritic cells.
00:22:43.24 This removes the lysosomal targeting signal from the invariant chain,
00:22:49.27 leaving a small segment of the invariant chain that is rapidly removed
00:22:53.14 by virtue of the activity of another class II associated chaperone,
00:22:57.26 not invariant chain, but something called HLA-DM,
00:23:00.28 that destabilizes the affinity of this remaining invariant chain fragment
00:23:05.04 to the peptide binding cleft of the class II molecule,
00:23:09.03 allowing the peptide to bind and displace the invariant chain derived peptide
00:23:16.24 and this then peptide MHC complex can go up to the cell surface.
00:23:21.19 I mentioned cystatin c before, it works at this stage by inhibiting
00:23:26.13 the activity of cathepsin s, it slows the cleavage, renders the cleavage less efficient
00:23:32.16 of the invariant chain making these molecules less accessible to peptide loading.
00:23:38.15 In a flow diagram in terms of what this means for membrane traffic,
00:23:43.05 here emanating from the golgi complex is the invariant chain class II complex,
00:23:48.06 enters endosomes and in immature dendritic cells nothing happens
00:23:51.27 because the level of cathepsin s is low, the activity of cathepsin s is low because
00:23:58.17 the activity of cystatin c is high and also the pH of these structures is not optimal,
00:24:04.17 and instead these class II molecules go to lysosomes. Maturation reduces
00:24:09.20 cystatin c activity, increases cathepsin s activity playing a role in helping
00:24:16.09 these class II molecules proceed on to the cell surface. Now the molecules
00:24:20.11 that had made it to lysosomes are there and also as long as the dendritic cell
00:24:26.15 remains immature not much happens. Here is a video taken by Amy Chow
00:24:32.28 in our laboratory a few years ago from a MHC molecule that has been linked
00:24:40.13 to the green fluorescent protein in immature dendritic cells, and what you
00:24:45.02 are looking at are lysosomes that are just sort of bouncing around, aimlessly
00:24:48.05 in these immature cells. So as I've mentioned earlier,
00:24:53.10 the class II molecules are there, the antigen is there and nothing is happening.
00:24:56.21 But very soon after adding LPS to this system, a ligand for a Toll-like receptor,
00:25:02.29 specifically TLR-4, you get a very different effect. Now what you can see
00:25:07.20 is that these lysosomes begin shooting out tubules and the lysosomes
00:25:13.17 start accumulating in a small dot depleting the amount of class II that is
00:25:17.29 associated with them and you can begin to see class II appearing on the surface
00:25:22.25 of the cell, all these events taking place really just over a time course of
00:25:27.20 a couple of hours. This is a video in which we are just able to visualize
00:25:31.24 the movement of some of these lysosome derived tubules from their site of
00:25:35.10 formation in lysosomes out to the periphery of cells and while I'm going
00:25:39.04 to show this to you, there are various biophysical techniques that you can use
00:25:42.05 to actually show that these tubules and vesicles derived from them will
00:25:45.22 physically fuse with the plasma membrane of the cell, delivering not only
00:25:50.15 the MHC class II molecule, but obviously also the antigen that has bound
00:25:55.28 to it as a consequence of the peptide loading event that took place
00:26:01.01 in the lysosome just at the moment of dendritic cell maturation.
00:26:05.08 All of these events take place as I said in just a couple of hours
00:26:09.07 if you wait overnight you can now see live dendritic cells that look ever much like
00:26:14.29 the static images I showed you earlier. Here a cell with all of its MHC class II molecules
00:26:21.24 on the surface, lysosomes are now stained red because none of the GFP
00:26:26.14 or green fluorescent protein coupled class II molecules are present within them anymore.
00:26:31.21 So what that means then is here one more unexpected feature of the system,
00:26:38.21 which is that MHC class II molecules can escape from lysosomes
00:26:43.21 to dendritic cell surface, by a pathway which we refer to as your retrograde transport pathway.
00:26:49.26 Anterograde transport refers to what happens when molecules
00:26:54.15 such as antigens come from the outside by endocytosis into the lysosomal compartment,
00:26:59.14 retrograde refers to what happens when they go out. Again, this is probably,
00:27:04.06 or almost certainly I should say, a microtubule driven process,
00:27:07.15 but whatâ€™s most remarkable is that it happens at all. Our conventional view of
00:27:12.00 lysosomes is really kind of summarized here in this early medieval representation,
00:27:16.19 even prior to Metchnikoff, showing that there is no escape.
00:27:20.25 This is at least the conventional view. Proteins, antigens, whatever microbes are collected,
00:27:28.03 delivered into lysosomes and simply degraded. So we had not really anticipated
00:27:34.12 that there was going to be a pathway anywhere in cell biology
00:27:39.12 that was going to allow us to recover or allow a cell such as a dendritic cell
00:27:45.04 to recover molecules in a very selective and very efficient fashion
00:27:49.19 so they can move from this degradative compartment out to the cell surface.
00:27:54.00 Now when they get out to the surface, why do they stay there?
00:27:58.03 Why don't they just come back into lysosomes by endocytosis.
00:28:01.05 Well you might say endocytosis is shut off and indeed, as I already mentioned,
00:28:05.22 it is as a consequence of down regulating active forms of Rho family GTPases,
00:28:11.29 such as Cdc42 and Rac, all of which are involved in actin assembly. So the normal
00:28:20.02 ability of immature dendritic cells to capture antigen by such processes
00:28:24.11 as macropinocytosis or phagocytosis, which are both strongly actin driven
00:28:30.18 processes as we've seen in the first video, indeed are turned off. But uptake
00:28:36.18 via endocytosis by clathrin coated pits, which are much smaller vesicular carriers
00:28:43.23 that can be formed about only 0.2 microns in diameter, as opposed to the
00:28:48.17 phagosome, which can be one or two or three or even five microns in diameter,
00:28:52.24 this pathway continues. And indeed we know that MHC class II molecules
00:28:57.19 can enter cells, and indeed can enter dendritic cells by clathrin mediated
00:29:03.00 endocytosis. So why is it that class II molecules do not enter in the mature cell?
00:29:11.27 That brings us to another emerging fundamental feature of membrane traffic,
00:29:17.11 and that is the role of protein based ubiquitination in controlling the movement
00:29:22.18 of membrane proteins from one compartment to the next. Over the last several
00:29:27.05 years, a large number of investigators have demonstrated that ubiquitin plays
00:29:32.21 a critical role in signaling, either the endocytosis of endocytic receptors into
00:29:38.09 clathrin coated pits and/or the ability of those receptors at the level of endosomes
00:29:44.08 to be sequestered into these rather oddly shaped structures
00:29:48.28 called multivesicular bodies. We know from the work of Scott Ember and others
00:29:54.09 for example that when ubiquitin is modified or a membrane protein is
00:29:59.12 modified by ubiquitin, after delivery or upon delivery to the endosomal compartment,
00:30:04.19 these ubiquitinated membrane proteins are further captured
00:30:08.25 by the endosome sequestered in these little internal vesicles that then
00:30:14.07 are delivered to late endosomes and eventually to lysosomes where they can finally
00:30:20.22 be degraded. Now this happens in dendritic cells because if you look actually
00:30:26.21 by electron microscopy in a picture taken by the late Marc Pypaert is shown here
00:30:35.11 that the class II molecules are not found on the limiting membrane of lysosomes,
00:30:40.11 but rather are found associated to a first instance with these internal vesicles.
00:30:46.09 Now this was a real surprise, a double surprise because we further thought
00:30:51.15 that of course not only everything that would go into a lysosome would be
00:30:56.06 degraded, but certainly everything that was associated with the multivesicular body
00:30:59.24 would be degraded somehow dendritic cells and class II molecules have figured this out.
00:31:05.20 Now this is how the ubiquitin system works, and I'll show you the solution
00:31:10.21 to this problem at least the first solution to the problem. Ubiquitin is a small
00:31:15.15 protein that is now well known as a consequence of a series or cascade of events
00:31:22.13 to be covalently linked to a variety of different acceptors both cytosolic proteins
00:31:29.02 as well as membrane proteins by virtue of the activity of at least two large
00:31:34.19 families of so called E3 ligases that fall either into the HECT family or
00:31:40.11 the RING family, the details of this at the moment are not important,
00:31:44.10 but what is important is that both of these E3 ligases can affix ubiquitin molecules
00:31:49.16 usually the lysine acceptors on a variety of different proteins.
00:31:54.04 Now it turns out that of all the MHC class II molecules that have been
00:32:00.26 sequenced so far thereâ€™s enormous diversity in terms of the sequences
00:32:04.28 that one finds in the cytoplasmic domains of these molecules
00:32:08.13 except for a single conserved lysine residue shown here at position 4 in the cytoplasmic domain
00:32:16.13 of the beta chain of the MHC class II molecule. When Jeoung-Sook Shin
00:32:21.06 who is now at UCSF as a faculty member was in my lab, she made this
00:32:27.02 realization and further surmised that gee if there is such an important
00:32:31.21 and well conserved lysine residue present in class II molecules,
00:32:35.15 perhaps class II molecules are subject to ubiquitination. And, indeed, not only
00:32:40.25 did she find that they are subject to ubiquitination, but that ubiquitination
00:32:45.01 is exquisitely well regulated. So here you are looking
00:32:50.09 at an SDS gel which was subjected to western blot antibody labeling procedure
00:32:57.16 to detect molecules of MHC class II that are either ubiquitinated or not ubiquitinated.
00:33:03.29 So here as you can see in immature dendritic cells class II molecules
00:33:07.26 on the beta chain are nicely ubiquitinated, but again, shortly after maturation
00:33:12.25 of these cells by stimulation of the Toll-like receptor system,
00:33:16.20 you now find that those ubiquitin molecules are no longer present on class II
00:33:22.18 we believe because they are no longer added but the most important
00:33:26.14 conclusion is that they are not there, and because they are not there,
00:33:30.03 they now lack the ability to enter the cell and become sequestered
00:33:34.06 in multivesicular bodies and in lysosomes. So the bottom line is that in
00:33:39.21 short dendritic cell because ubiquitination does not occur,
00:33:43.09 those MHC class II molecule peptide complexes that are recovered by retrograde transport
00:33:49.16 from the lysosomal compartment to the plasma membrane stay put
00:33:53.19 because they lack the information, namely the ubiquitin molecule
00:33:57.02 linked to the class II that happens in immature dendritic cells.
00:34:00.23 They lack this ubiquitin molecule and as a consequence these class II peptide complexes
00:34:06.08 stay where they can best serve the interest of the immune system
00:34:10.07 and be available for recognition by Cd4 positive T-cells.
00:34:14.09 And this is what that looks like. Dendritic cells shown here in red
00:34:19.19 can complex with an enormous number of T-cells because they express
00:34:24.29 at such high levels these MHC peptide complexes in the case of class II because
00:34:31.06 those complexes cannot be internalized after maturation by endocytosis.
00:34:37.12 Class I is a different story, and I'd like to turn to that now because it illustrates
00:34:43.07 another aspect of the system as why dendritic cells are indeed so special,
00:34:48.15 not only in terms of the role they play in the immune response,
00:34:52.17 but how that role is determined by alterations, in fact some rather
00:34:57.28 unexpected alterations in membrane traffic.
00:35:01.22 Now class I as I've already mentioned is a pathway that is mostly adept
00:35:09.16 to dealing with endogenous antigens. So the best example I can give you
00:35:15.23 is if you have an influenza virus infection and epithelial cells in your airway
00:35:23.19 are infected by influenza virus, those cells are going to be making
00:35:29.12 lots of proteins that are encoded by the virus. Those proteins are going to be degraded
00:35:34.22 in the cytosol, again following a ubiquitination event they'll be degraded
00:35:38.18 by the proteosome in the cytosol, small peptides generated from
00:35:43.03 those ubiquitinated proteins and then those small peptides translocated
00:35:48.24 into the lumen of the endoplasmic reticulum by virtue of the activity of a rather
00:35:54.04 remarkable ATP-driven membrane peptide transporter called TAP, actually TAP1 and TAP2.
00:36:03.06 So the peptide that enter into the ER are loaded onto class I molecules
00:36:07.13 and then they make their way out to the cell surface by the constitutive secretory pathway.
00:36:13.02 Now there's a flaw in this logic. Remember I told you that only dendritic cells
00:36:17.08 can start an immune response. And I also just told you that the predominate cell,
00:36:22.25 in fact possibly the only cell that is infected after you become infected by
00:36:30.03 influenza are epithelial cells. How do we guard ourselves against
00:36:36.10 the possibility that the dendritic cell doesn't become infected?
00:36:39.00 The epithelial cells are incapable of generating a robust T-cell response,
00:36:43.10 only the dendritic cells are capable of doing that but the dendritic cells are not infected,
00:36:48.16 they're not making the influenza virus specific proteins. So how do
00:36:54.13 dendritic cells deal with this? They deal with it by having developed
00:36:57.26 a rather remarkable system of membrane transport,
00:37:03.00 which is classically referred to as cross presentation. It was really first described
00:37:07.08 by an immunologist, Mike Bevan. Here it was thought to be the case
00:37:12.04 that antigens coming in from the outside rather than being restricted
00:37:16.29 to the MHC class II pathway can cross over and in fact have access to the class I pathway
00:37:23.00 and do so by somehow breaking out of the endosome lysosome system,
00:37:27.03 entering into the cytosol and becoming accessible to the ubiquitination proteosome
00:37:32.06 degradation system that then is also responsible for servicing
00:37:37.16 those antigens that are endogenously synthesized by the cell. So the peptides
00:37:43.20 that form from these cross presented antigens can enter into the ER lumen
00:37:49.09 via the TAP1 TAP2 translocator, be loaded onto class I molecules
00:37:54.29 and then as I've been describing, make it out to the cell surface.
00:37:58.09 So the way this probably works in practice in the case of virus infections
00:38:02.23 is diagrammed here, immature dendritic cells will capture and take up
00:38:08.27 just as another phagocytic load a virus infected cell, which has been killed
00:38:15.08 by virtue of its virus infection. So dead cells, apoptotic cells, necrotic cells
00:38:21.06 can be nicely recognized by dendritic cells, enter into phagosomes,
00:38:25.09 these cells are then degraded and then antigens derived from the infected cell,
00:38:30.00 most importantly the virus encoded antigens now come out into the cytosol
00:38:35.04 and can be degraded by the proteosome system and be presented on the surface
00:38:39.23 of the dendritic cell on class I molecules. Now remember while all this is going on,
00:38:46.10 proteins that are also intrinsic to this self of the infected cell,
00:38:52.14 in other words our own proteins, are not going to be immune to this,
00:38:56.01 they will also be degraded in the phagosome and some portion of them
00:39:00.25 we have to imagine will also come into the cytosol and be degraded
00:39:05.18 and be loaded onto class I molecules and presented to now
00:39:09.15 CD8 positive T-cells on the cell surface. So how is it then that
00:39:13.24 the dendritic cell can distinguish between the viral antigen and the self antigen?
00:39:18.08 How does the immune system do this? How does the immune system do that?
00:39:22.29 Now it may be apparent to some of you, but I actually had to go off
00:39:25.29 and think about this for a little bit, but it turns out that to understand
00:39:29.22 how the immune system balances tolerance and immunity responses
00:39:33.18 to self versus non-self actually has a lot again to do with dendritic cells,
00:39:38.02 specifically the property of dendritic cell maturation which we now should
00:39:42.00 come back to and look at in a little bit more detail to understand just how
00:39:45.12 these cells via the process of maturation controls the progress of the immune response.
00:39:50.21 Now remember that maturation links the two major arms of the immune system,
00:39:55.24 the innate immune response to the adaptive immune response
00:39:59.13 by detecting microbial pathogens and then turning those pathogens into
00:40:04.03 the peptides that are required to be presented to T-cells to generate adaptive immunity.
00:40:08.05 Now the maturation process itself in its first instance is controlled by this family
00:40:14.15 of Toll-like receptors that I've mentioned, that essentially act as barcode readers
00:40:19.01 and I'll come back to that in a moment, that identify and deconstruct exactly
00:40:24.16 what type of pathogen happens to be present at the time the maturation event is induced.
00:40:30.28 Now there are a number of different Toll-like receptors. Some of them are
00:40:34.15 diagrammed here. About 12 or more, I've lost count since it changes periodically,
00:40:40.19 and what these Toll-like receptors are for is that they are specific for a variety of
00:40:44.13 different components that one finds in a wide variety of different pathogens.
00:40:47.19 You find some of the Toll-like receptors expressed on the plasma membranes
00:40:51.10 of cells, other Toll-like receptors are expressed in endosomes and lysosomes.
00:40:55.05 They are specific for bacterial proteins, bacterial lipids, one of the proteins
00:40:59.14 is one called flagellin, which is the major component of the bacterial flagella.
00:41:03.14 LPS is a major lipid species found in cell walls of many bacteria,
00:41:09.25 but many of the intracellular Toll-like receptors in particular actually react with specifically
00:41:15.28 and identify specifically nucleic acids, both single stranded and double stranded RNA and DNA.
00:41:22.27 In all cases, the general property that is elicited is this property of maturation,
00:41:28.17 but not all forms of maturation are created equal because not all
00:41:32.07 Toll-like receptors are created equal, and in fact they transmit different types
00:41:36.18 of signals to the dendritic cell. So as I said, these receptors work together
00:41:41.17 in the sense of a bar code. Some firing, others not firing, depending upon
00:41:46.12 what pathogen happens to be present, and the dendritic cell reacts to this information
00:41:51.22 and undergoes a path of its own maturation that adapts itself specifically
00:41:57.28 to the type of immune threat that is coming in from the environment
00:42:02.00 again and identifies the nature of the pathogen, the nature of the threat based
00:42:06.27 on the combinatorial array of Toll-like receptor ligands that happen to be present
00:42:13.06 and associated with that particular bacterium. Now as a consequence
00:42:17.27 of detecting these different arrays of Toll-like receptor ligands,
00:42:24.04 the dendritic cell matures and what it does as a consequence of that is
00:42:30.03 of course is to secrete a wide variety of different cytokines, which are again
00:42:33.16 essentially immunological hormones. Now T-cells are very smart, they are
00:42:39.27 almost infinitely capable of recognizing a wide array of different types
00:42:45.08 of antigens. But they have to essentially be told what to do by the dendritic cell
00:42:51.21 and this is not only by virtue of identifying the particular peptide MHC complex
00:42:57.01 that is presented by the dendritic cell that actually gets the T-cell responses going,
00:43:01.08 but this mixture of cytokines that is released by dendritic cell specifically
00:43:06.05 and in a customized fashion depending upon the type of microbe that was detected
00:43:12.19 is that which actually determines what the overall differentiation of the T-cell is going to be.
00:43:19.16 So its not enough simply to stimulate T-cells as a consequence
00:43:23.05 of having them detect via the T-cell receptor, the peptide MHC complexes
00:43:27.24 that are formed by dendritic cells, but the dendritic cells add to that process
00:43:32.21 by transmitting their experience of what type of pathogen had come in,
00:43:38.14 and they do this in this case by secreting the characteristic cytokines.
00:43:42.14 So one example of this is certain types of Toll-like receptors, or stimulation by
00:43:48.29 Toll-like receptors will cause dendritic cells to release the very
00:43:53.05 potent immunogenetic cytokine, IL-12, or interleukin 12.
00:43:57.27 T-cells that detect antigen exposed on the surface of
00:44:03.10 a dendritic cell that is secreting interleukin 12 undergo a type of differentiation
00:44:08.09 that allows them to become a particular sub-class of T-cell called Th1 T-cells,
00:44:14.04 which are highly inflammatory and highly immunogenetic cells.
00:44:17.16 Now the way this looks actually in situ is shown nicely here. This is a
00:44:22.06 scanning electron micrograph showing a dendritic cell in the background
00:44:25.26 with a number of T-cells that are attached very closely, as I've shown you
00:44:31.19 earlier in one of the video images, T-cells move around quite a bit across
00:44:36.07 the surface of dendritic cells, but when they finally find a good match,
00:44:40.17 a peptide MHC to a given T-cell receptor, they have a tendency to stay there
00:44:45.14 and stay there for a fairly long period of time, hours if not more,
00:44:51.08 and over this period of time they are literally bathed in the cytokine mix
00:44:56.04 that is being released by the dendritic cell, instructing them to become
00:45:00.22 a wide array of T-cells that all recognize antigen but all have a very very different
00:45:07.27 functional outcome with respect to how the immune response works.
00:45:11.09 I've lifted some of the more popular T-cell types that one can find.
00:45:15.08 We won't go through them in any detail at all, but just simply to say that
00:45:20.11 there are many many different possible T-cell outcomes that have different effects
00:45:25.03 on the so CD8 killer cells, or cytotoxic T-lymphocytes,
00:45:30.25 CTLs are ones that actually kill their target, so a cell that is infected by a virus
00:45:37.21 as we've discussed before will be killed by a cytotoxic T-cell of this particular type.
00:45:44.11 Not any T-cell will do this, but in fact only these will. CD4 helper cells help
00:45:49.19 generate antibody responses by working in collaboration with B-cells.
00:45:53.22 Inflammatory cells, central memory, effector memory cells are all T-cells that
00:45:58.14 circulate retaining the information of the immune account that had occurred,
00:46:03.16 retaining the lessons learned from the dendritic cell, and finally one
00:46:07.06 that we'll come back to in just a moment is the regulatory T-cell,
00:46:10.03 which rather than promoting immunity, actually dampens immunity and
00:46:13.13 probably assists or plays a central role in assisting the process of tolerance.
00:46:18.04 Again, often these cells are generated by dendritic cells, but not always,
00:46:24.17 and I think here I'd like to turn to just this very issue of tolerance and recognition
00:46:31.10 of self or non-self. How does it work? Basically it works in two settings,
00:46:36.10 before birth and early after birth, in the organ called the thymus where all
00:46:44.25 T-cells have their origin, prior to the exposure of the developing fetus or organism
00:46:51.07 to any exogenous antigens at least under normal circumstances,
00:46:55.08 a critical process called negative selection occurs. Now during negative selection,
00:47:00.05 either dendritic cells in the thymus or a related but nevertheless different
00:47:05.03 type of cell which has the same function or is presumed to have the same function
00:47:09.27 in the thymus called thymic epithelial cells have the remarkable function
00:47:15.06 of being able to turn on at the level of transcription, the expression of a wide array
00:47:22.00 of almost all of the proteins that we know that will be expressed in differentiated cells
00:47:27.03 later in life in the pancreas, in the liver, in the kidney, all of these are
00:47:32.22 expressed by these cells early on in the thymus, creating peptide MHC complexes
00:47:38.02 that are recognized by these thymocytes or forming T-cells that are being born
00:47:45.11 and developing in the thymus at this very very early stage of life. Now what
00:47:50.21 happens at this stage though is really quite interesting
00:47:53.21 and also quite important, and indeed quite profound.
00:47:56.14 Rather than the recognition event of the cognate peptide MHC by the T-cell receptors
00:48:04.11 on these developing T-cells, rather than causing an immune response or
00:48:09.28 an unrestricted proliferation of the T-cells, instead the T-cells
00:48:14.02 are induced to undergo apoptosis and die. In immunological parlance,
00:48:20.03 these cells are referred to as deleted. So any T-cell that recognizes
00:48:24.18 its antigen in the environment of the thymus early in development
00:48:29.06 is negatively selected and removed from the repertoire of
00:48:36.28 all of the antigens that could possibly be seen by the T-cell receptor later in life.
00:48:43.06 So this is a terrifically important first pass, whereby the immune system,
00:48:48.07 thymic and epithelial cells and dendritic cells due to the special properties of the thymus,
00:48:53.17 which are still not quite understood, are capable of removing a wide array
00:49:00.08 of T-cell specificities that would otherwise recognize host or self proteins
00:49:07.03 causing auto-reactivity and auto-immunity. As powerful and as important
00:49:13.07 as this process is, its not 100% efficient. Some self antigens are missed,
00:49:18.20 but another critically important class of antigen that's missed
00:49:23.11 is environmental antigens, since after birth we are all bombarded
00:49:28.13 and in fact bathed in a wide number of environmental allergens such as pollen in the air,
00:49:35.07 food allergens of various types, things that may penetrate through the skin,
00:49:40.17 and if we were to amount an immune response to each one of these foreign
00:49:44.08 antigens we would be hyper-allergic and not be in a very good state.
00:49:50.14 Now there is no way that the thymus can educate our T-cell responses or
00:49:54.29 the dendritic cells can educate our T-cell responses in the thymus
00:49:57.27 to delete T-cells that might be specific for a pollen or environmental antigens.
00:50:04.25 That has to occur after birth because obviously as a fetus we are not generally
00:50:09.16 speaking exposed to too many environmental antigens that are allergic in this sense.
00:50:14.05 So this is a process that's been left to the formation of this final and critically
00:50:21.21 important and yet incredibly poorly understood form of T-lymphocyte
00:50:26.10 called the T reg, or regulatory T-cell. Now a lot of these are in fact formed
00:50:31.12 in the thymus, so in addition to deletion of T-cell reactivities, one also finds
00:50:36.24 that the thymus will produce an array of regulatory T-cells that recognize
00:50:42.18 a variety of self antigens that will then have a tendency to help turn off
00:50:48.01 T-cell responses that occur inappropriately later. Okay, but many regulatory T-cells,
00:50:54.26 or T regs, are not produced in the thymus but rather are produced in the periphery
00:50:59.26 as a consequence of not so much a negative selection process but a tolerogenic
00:51:04.25 process which in this case is mediated almost exclusively by the dendritic cell
00:51:09.11 not by the thymus. Now this happens under steady-state condition.
00:51:13.27 So what I mean by that is if an antigen is encountered by dendritic cells that have not
00:51:21.09 received a stimulus via a microbial type Toll-like receptor ligand to mature,
00:51:29.22 what one finds then is that all of the same processes of antigen processing
00:51:34.12 and presentation and transport of the peptide of MHC complexes
00:51:38.10 to the surface take place, dendritic cell develops to a form that is capable of efficiently
00:51:44.09 doing this and efficiently generating T-cell recognition, but nevertheless
00:51:49.14 under these conditions in the absence of a Toll-like receptor stimulus
00:51:53.18 or another inflammatory stimulus, the type of T-cell that emerges is a
00:51:59.03 regulatory T-cell, or an induced regulatory T-cell, totally as a consequence
00:52:03.06 of peripheral recognition events. So these T regs instructed again and formed
00:52:09.26 almost uniquely by peripheral dendritic cells found in our lymph nodes,
00:52:15.05 lymphoid organs and indeed all of our peripheral tissues are our last line
00:52:21.12 and in many cases our most important line of defense against mistakes
00:52:26.21 that can be made by the immune system between self and non-self,
00:52:31.11 between foreign and endogenous antigens. Again, serving to control
00:52:36.09 this balance between tolerance and immunity. Again, it is the T-cell that does it,
00:52:42.13 although to be fair we don't really understand very much about how T regs work,
00:52:47.10 this is an emerging field, an emerging problem at the moment.
00:52:51.11 But what it does seem to be quite clear based on genetic deletion results
00:52:56.04 and antibody blocking results that have been done quite recently, it is these
00:53:01.04 dendritic cells that exist under steady state non-inflammatory conditions
00:53:05.10 that really are responsible for generating these T regs.
00:53:09.21 Now this is critically important for a variety of reasons because every time a
00:53:14.19 dendritic cell matures as a consequence of being stimulated by Toll-like receptor
00:53:19.24 ligand, those dendritic cells present not only the foreign antigen
00:53:23.18 but also present every self antigen in the body that they can come in contact
00:53:27.26 with over that period of time. So every time we respond to a foreign stimulus,
00:53:33.23 we run the risk of responding to one of our own self antigens
00:53:38.21 and run the risk of developing auto-immunity. So in order to maintain
00:53:45.06 this very very careful relationship, this very very careful balance
00:53:50.07 that must occur lest auto-immune pathologies set in between immunity and tolerance,
00:53:57.13 there is this continuing production of T regs that occurs that provide with us
00:54:03.20 this important break, this important line of defense to maintain equilibrium,
00:54:09.07 maintain homeostasis, and maintain health. So the way I like to frame this
00:54:15.16 is as a hypothesis, which I stress by saying is really no more than a hypothesis
00:54:22.06 at this point, but nevertheless I think summarizes quite well the process as many
00:54:27.20 of us really believe it occurs at this point. So as I was saying,
00:54:32.00 under conditions of no infection, under the steady-state, one finds
00:54:35.28 immature dendritic cells in peripheral tissues, as shown here in the skin,
00:54:40.02 again using the same diagram we've been looking at during the course of these two lectures.
00:54:45.11 No infection, immature in the periphery, and at some point these cells
00:54:51.09 either just due to stochastic processes or due to some inductive process
00:54:56.11 migrate from the skin via the lymphatics into the lymphoid tissues.
00:55:00.22 Along the way, they undergo a type of maturation, because now in lymphoid
00:55:06.11 organs they are capable of presenting antigens, all self-antigens in this case,
00:55:10.17 or all environmental antigens, but nevertheless the type of maturation
00:55:14.20 that they undergo is one that leads to tolerance. So they are not antigen
00:55:19.08 presenting, they are not very effective antigen presenting cells as immature cells
00:55:23.21 in the periphery, they are much better at it when they are in lymphoid organs
00:55:27.18 but they are nevertheless still tolerogenic. Again, these are conditions under
00:55:31.11 steady state, meaning no infection, no inflammation. Everything changes though
00:55:36.04 when we go to the condition of infection, or inflammation. Here now
00:55:41.10 what you find is that again the dendritic cells are still immature in the periphery,
00:55:45.23 but now they encounter a Toll-like receptor stimulus as a consequence
00:55:50.16 of the advent of one or more microbes as we've been discussing. The migration
00:55:56.29 process is the same, the delivery to lymphoid organs is more or less the same,
00:56:01.14 but now the maturation that takes place is one which is not tolerogenic but rather immunogenetic.
00:56:08.19 Okay, so the T-cells that are produced by this same progenitor population of
00:56:14.22 dendritic cells, possibly, possibly there are subsets, but possibly the same
00:56:19.09 progenitor population of dendritic cells under conditions of infection,
00:56:23.11 under conditions of inflammation, yields T-cells that undergo development
00:56:27.05 not to produce T regs, but rather to produce one of the many types of
00:56:30.28 inflammatory or immunogenetic T-cells that I listed for you just a moment ago.
00:56:36.12 Now this to me comprises probably one of the most profound of all problems that
00:56:44.16 remain in the immune system. I've stated it in what may appear to some of you
00:56:49.23 at least to be relatively reasonable terms, but the fact of the matter
00:56:53.04 is we have almost no idea how these events are interconnected.
00:56:57.18 We know small details, all of which are indeed enticing, beginning with why
00:57:03.14 is it that transcriptionally one can find so many different differentiated gene
00:57:07.28 products expressed early on in the thymus? We know something about what
00:57:12.18 the transcription factors are that do this, but how all of this is regulated,
00:57:15.26 how it actually works, very very few of the details are really known,
00:57:20.03 and it really represents a terrific area for research of basic biology and also to
00:57:25.26 come up with still solutions to one of the great problems left in immunology.
00:57:31.19 There are many, but this is certainly one that tops my list. Now another reason
00:57:37.16 why this is so important is not just because of the basic biological aspect,
00:57:42.03 but also because of the disease aspect. I think increasingly as size progresses
00:57:47.21 in our understanding and our ability to do more and more complex experiments,
00:57:52.23 particularly at the systems level, an equally valid path to take in studying basic
00:58:00.10 biology is to understand disease processes. This of course has been done
00:58:05.03 by many in the past, but I think increasingly so at earlier and earlier stages
00:58:09.00 in ones scientific career and ones scientific interests, its possible to begin
00:58:14.03 to do real basic solid experiments where your question is what happens during
00:58:20.02 a particular disease process. So how does tolerance and immunity
00:58:23.18 fit into this? I've already hinted at it several times, but if you have a situation
00:58:28.06 where there is too little tolerance in other words the dendritic cells
00:58:32.10 or the thymus were not optimally efficient at deleting auto-reactive T-cells
00:58:37.24 or turning auto-reactive T-cells into T regs, or regulatory T-cells,
00:58:43.00 one can find a wide variety of diseases that fall into the broad class of auto-immune disorders,
00:58:49.24 such as auto-immune diabetes, lupus, or Myasthenia gravis. These are mediated
00:58:55.04 either by the production of pathogenic antibodies to self proteins,
00:58:59.08 or T-cells that exert direct cytotoxic effects on normal host tissues.
00:59:05.24 Another possibility is chronic inflammation, so diseases such as arthritis,
00:59:11.19 or asthma, Crohn's disease, ulcerative colitis, Multiple Sclerosis, possibly
00:59:16.22 have to do with the fact that an inflammation starts and then can't be turned off.
00:59:20.28 These may not be strictly auto-immune in many cases because for a lot of these
00:59:26.00 diseases there may not be a single antigen against which T-cells continuously
00:59:30.21 are producing new antibody via B-cell production or new cytotoxic secretions
00:59:39.03 as a consequence of the T-cells own activities, but nevertheless these
00:59:43.17 are processes that keep going because of disregulation of the balance
00:59:48.27 between tolerance and immunity. And again, in many ways one can attribute
01:00:00.00 the brute cause of all of this to dendritic cells misbehaving,
01:00:04.25 presenting antigens in the wrong context, producing the wrong type
01:00:08.26 of T-cells under a condition that doesn't call for that type of T-cell response,
01:00:13.24 and then the do-loops that emerge simply don't get turned off.
01:00:17.27 So how do we intervene in all of these things and how can we do this not only to
01:00:24.09 understand the biology, which is of course paramount, but also to understand
01:00:28.00 how therapeutically we can begin to intervene in these diseases processes
01:00:32.16 with ever higher degrees of specificity and exactness so that we can turn off
01:00:38.04 just the disease process and not interfere with normal ongoing processes
01:00:43.04 or actually do more harm than good. So now that I've moved myself from
01:00:48.23 academia to a biotech company, these are problems that are coming to the fore
01:00:54.23 on a daily basis, and its of no small matter to try and understand and grapple
01:01:01.28 with these problems, not only as a basic scientist but also as someone
01:01:06.06 who is now committed to understand how it is that you can turn that
01:01:10.07 basic science knowledge into dealing with major major health problems such as these.
01:01:15.09 It's also possible that you have too much tolerance and two sets
01:01:21.17 of very bad things can occur under these circumstances. This is different from diseases
01:01:27.05 that lead to immunodeficiency. Here you have diseases where the immune system
01:01:32.16 is often intact, but has been educated by the pathogenic organism
01:01:38.21 or as shown here by cancer cells, to evade the immune response. Cancer is I think
01:01:47.01 a particularly challenging example. Immunotherapy in cancer is something
01:01:51.16 that is now just starting to gain steam now with the first immunotherapeutic
01:01:56.28 to prostate cancer just having been approved this year, but what we
01:02:02.00 understand about cancer and the immune system tells us, at least to a first approximation,
01:02:07.25 that many cancers in fact are capable of generating immune responses,
01:02:11.14 either due to mutation or to ectopic expression of proteins that are not normally produced by a given cell.
01:02:20.03 Cancer cells in fact can elicit T-cell responses, but they've figured out,
01:02:25.12 or if they haven't figured out at least they've been selected for cells that are
01:02:29.25 capable of subverting those T-cell responses, either by turning them off,
01:02:34.02 such that when the T-cell penetrates into a tumor bed and tries to kill its target,
01:02:39.00 the target protects itself by secreting or placing on its surface molecules that in
01:02:45.05 fact will abrogate T-cell responses rendering them as immunologically, I'll just say, anergic.
01:02:53.21 Another possibility though is that cancer cells in fact by much the same way that
01:02:59.26 dendritic cells seem to do it, will seem to generate a T-regulatory or T reg responses,
01:03:05.15 again having the same effect subverting T-cell responses to cancerous cells
01:03:12.10 that would otherwise be amenable to be controlled by those T-cells, at least in theory.
01:03:18.10 Another, and I think in many ways more clear example, occurs in the case of many
01:03:25.01 chronic viral infections, such as CMV or HIV. CMV is a particularly good example,
01:03:31.25 but many other chronic viruses are as well. What happens in these cases is that
01:03:37.00 viruses have figured out how to down regulate proteins on the surface of
01:03:43.10 the infected cell, or in some cases even on the surface of dendritic cells
01:03:47.06 in such a way as to prevent, again, T-cell recognition or in some cases even T-cell responses.
01:03:54.15 The immune system in a sense gets educated to understand that the viral proteins
01:03:59.21 are not actually foreign, but indeed are part of the own host protein repertoire,
01:04:09.04 and as a consequence by tricking the immune system in this way,
01:04:12.12 the virus can replicate and can maintain its infection with impunity without
01:04:19.19 risk of detection by the immune system. So in the case of diseases where
01:04:24.29 there is too much tolerance, therapeutic intervention that one can imagine,
01:04:30.04 is how is it that you reactivate T-cell responses by convincing the dendritic cells
01:04:36.24 to break tolerance as we say and re-introduce antigens either derived from cancer cells
01:04:43.21 or from viruses under conditions that now can generate positive
01:04:48.15 immunogenic immune responses rather than just tolerogenic immune responses.
01:04:54.05 So both of these types of disease states, again, embody I think some of the most exciting
01:05:00.02 biology, both immunology and cell biology that one can think of
01:05:05.00 in the immune system, plus also offer the opportunity to the lucky and interested
01:05:10.09 scientists, which hopefully includes me, to understand how it is one can
01:05:17.00 actually make either biological agents or even small molecule drugs
01:05:21.13 to either induce tolerance under conditions where you would like to turn off
01:05:26.20 chronic inflammation or turn off auto-immunity or overcome tolerance
01:05:31.17 under conditions where you would like to re-activate the immune system,
01:05:35.08 re-educating it to go about its job and combating what are effectively
01:05:41.24 foreign agents such as cancer or chronic viruses both for therapeutic benefit. Thank you.

Videos in this Talk

Part 1: Cellular Basis of the Immune Response
Audience:
- Researcher
- Educators of Adv. Undergrad / Grad
Part 2: Antigen Presentation and Dendritic Cells
Audience:
- Researcher
- Educators of Adv. Undergrad / Grad

Speaker: Ira Mellman

Total Duration: 1:32:05

Recorded: September 2008

Educator Resources for this Talk

All Talks in Immunology

Talk Overview

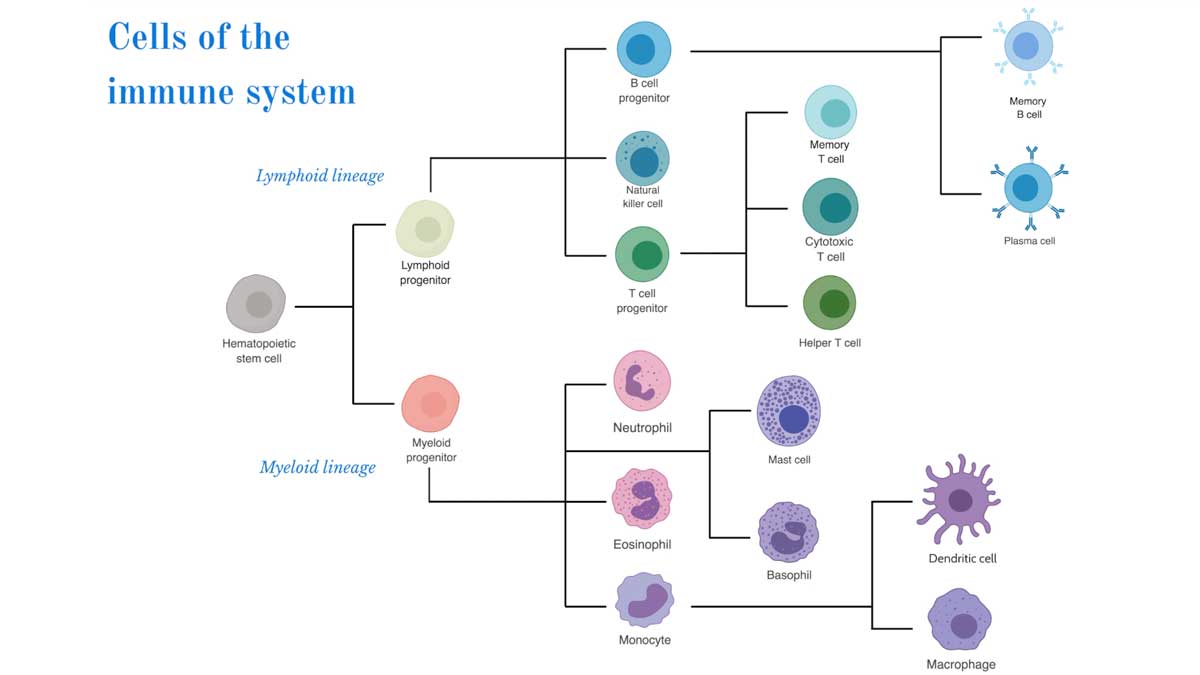
The immune system is charged with protecting us from invading microorganisms, a task that falls to a complex array of highly specialized cell types spread throughout the body but that must work together as an integrated system. How they accomplish and perform their functions can be wonderfully understood by probing the basic mechanisms governing their activities. In the first video, we will consider the overall organization of the immune response in cellular terms, the innate immune system (comprising evolutionarily ancient phagocytic cells that recognize conserved molecules of microorganisms) and the adaptive immune system (composed of lymphocytes that recognize chemically diverse antigens).

The immune response integrates two distinct systems of innate and adaptive immunity discovered over 100 years ago. Linking these two arms of the immune response is the task of a comparatively recently identified cell type, the dendritic cell. Dendritic cells have the capacity to detect the conserved microbial products that activate cells of the innate immune response and capture the dramatically wider diversity of microbial antigens to prime antibody and T cell responses characteristic of adaptive immunity. The unique capacity of dendritic cells for antigen processing and presentation reflects a series of remarkable specializations of basic principles of cell biology.

Speaker Bio

Ira Mellman

Ira Mellman is Vice President of Research Oncology at Genentech. Ira is a cell biologist with a long standing interest in membrane traffic. His lab is reponsible for key observations leading to the initial discovery of endosomes, the mechanisms of epithelial cell polarity, and the cellular basis of dendritic cell function. Until 2007, Ira was… Continue Reading

Comments

Shawn Freyssonnet-Inder says

January 21, 2019 at 9:08 pm

In this video (), I had a hard time reading some of the labels in the graphics even in full screen mode on my 17 inch mac book pro (I have 20/20 vision). Is it possible to get better than 240p quality?

Reply

Part 1: Cellular Basis of the Immune Response

Part 2: Antigen Presentation and Dendritic Cells

Talk Overview

Speaker Bio

Ira Mellman

Comments

Leave a Reply Cancel reply

Find a Video

Topics

For Educators

Educators Recommend

Techniques

Free Courses

Career Development

Our Favorites

Connect with Us

Talk Overview

Speaker Bio

Ira Mellman

Playlist: Allergies and Inflammation

Related Resources

Reader Interactions

Comments

Leave a Reply Cancel reply

Footer

Find a Video

Topics

For Educators

Educators Recommend

Techniques

Free Courses

Career Development

Our Favorites

Connect with Us