Fish in the Matrix: Neuronal Activity and Animal Behavior in Virtual Environments

Talk Overview

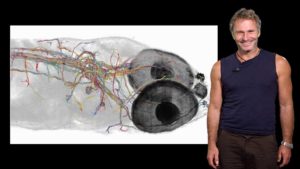
How does the brain translate sensory stimuli into a behavior? In his first iBiology talk, Dr. Florian Engert explains that larval zebrafish are an excellent model to tackle this question. Larval zebrafish are tiny, translucent, and genetically tractable vertebrates.  By making transgenic fish with labelled neurons, it is possible to visualize neuronal activity in the entire brain of a living and awake fish.  Engert introduces the virtual behavior simulators that his lab members use to trigger and measure neuronal activity in the fish.

Neuronal activity can be triggered by either external stimuli or by stimuli that are a result of your own actions.  In his second talk, Engert explains how his lab measured and compared neuronal activity in response to these two types of stimuli. Using a set up where larval zebra fish are immobilized with drugs, yet the neurons which innervate the muscles fire normally, they measured neuronal activity in response to visual stimuli. By moving a virtual landscape quickly or slowly they could mimic fast or slow swimming by the fish.  Interestingly, they found that the fish would adjust its neuronal activity up or down so its perceived swim speed matched the movement of the virtual landscape or, in other words, so the external stimuli matched the expected result of its actions. Engert’s group mapped the neurons responsible for visual processing and locomotion, as well as those responsible for gain control up or down to match the fish’s swimming strength with the external stimuli.

In his final talk, Engert describes work done with collaborators to develop a robust operant learning assay for larval zebrafish.  Using this assay and techniques for measuring neuronal activity in tethered, awake fish, they are beginning to decipher what happens in a vertebrate brain while the animal is learning.

Speaker Bio

Florian Engert

Dr. Florian Engert is a professor of Molecular and Cell Biology at Harvard University where he studies neural circuits using zebrafish larvae. Originally trained as a physicist, he received his PhD from the Ludwig Maximilian University of Munich in 1997. Engert transitioned into a career in neuroscience as a postdoctoral fellow at the Max Planck… Continue Reading