Talk Overview
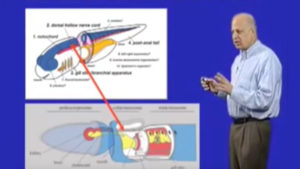
In the Introduction: Vertebrate body plans and the odd phylum of Hemichordates, I discuss the largely anatomical features that we use to identify the Vertebrates as a Subphylum or the chordates as a Phylum. These include such commonly perceived anatomical features, as the blocks of muscle around our trunk, called somites and tail. I also discuss some less obvious features, such as the notochord, a cartilaginous rod found in fish and found at least embryologically in every vertebrate. How did these originate from simpler organisms? I introduce a primitive related phylum, the hemichordates, and a particular animal, the acorn worm. In Part 1: The origin of the vertebrate nervous system: the Hemichordate perspective, I discuss why vertebrates ended up with a centralized nervous system that is highly organized from head to tail. It is surprising that the acorn worm has many of the patterning features of the vertebrate brain and centralized nervous system, although it has neither of these structures.
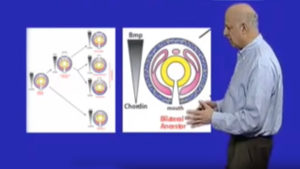
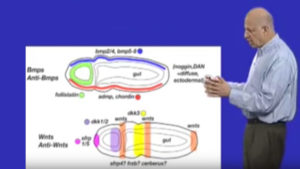
In Part 2: Telling the back from the front or what the chordates invented, I discuss why we look like invertebrate animals turned upside down, i.e. vertebrates have their central nervous system on their backs and invertebrates have it on their bellies.
In Part 3: How chordates got their chord, I discuss how the overall body plan of vertebrates, arose from the invertebrates based on knowledge of the commonalities in their developmental mechanisms. Here again, the acorn worm, offers the key comparison, being close enough to us to share some recognizable features, but far enough away to indicate the direction from whence we came.
Speaker Bio
Marc Kirschner

In 1993, Dr. Marc Kirschner joined Harvard University where he became the founding chair of the Department of Cell Biology. In 2003, he moved to Harvard Medical School to found the Department of Systems Biology. Research in Kirschner’s lab focuses on problems that require the coordination of biological events in time and space. His lab… Continue Reading





Leave a Reply